In terms of geometry and trigonometry, ASA and AAS are two different terms that describe different parts of a triangle.
The triangle is one of the basic shapes in geometry. The difference between ASA and AAS is that ASA refers to the angle opposite the side where the angle is adjacent to, while AAS refers to the angle opposite the side where it is acute. Both are used in geometry and trigonometry, but their meanings are different. So what are the other differences between ASA and AAS?
The article will focus on the difference between ASA and AAS, the usage of ASA and AAS, and how they are used in triangle congruence.
Summary Table
| ASA | AAS |
| Stands for Angle-Side-Angle | Stands for Angle-Angle-Side |
| Is a proof technique used in triangle congruence | Refers to the same theorem as ASA but is used when all three of the sides in one triangle are congruent to the corresponding sides in another triangle |
| A method of proving congruence | More of a method of proving similarity |
| Usually uses only geometry | Usually uses both geometry and trigonometry |
| Is also defined as the angles formed by two lines with the same transversal with no included angle | Is also defined as the angles formed by two lines with the same transversal and an included angle |
| Involves the formula A=B-C | Involves the formula C=A-B |
| Involves the values of the angles between 0° and 180° | Involves the values of the angles between 0° and 360° |
Definitions
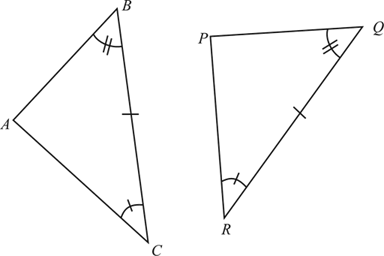
What is triangle congruence?
Before we go to the definitions of ASA and AAS. We need to know what triangle congruence is because ASA and AAS are closely related to the triangle congruence theory.
Triangle congruence is a method of proving that two triangles are congruent (equal) using only the lengths of the sides. This is done by showing that the angles in one triangle are equal to the angles in another triangle and that the lengths of the sides of one triangle are equal to the lengths of the sides of another triangle.
What is ASA?
ASA stands for Angle-Side-Angle. It is a proof technique used in triangle congruence. The ASA theorem states that if two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.
What is AAS?
AAS stands for Angle-Angle-Side. AAS refers to the same theorem as ASA, but it is used when all three of the sides in one triangle are congruent to the corresponding sides in another triangle. In AAS, it is not necessary to show that the angles are congruent.
Which one should I use?
It is usually easier to use ASA because it does not require the lengths of the sides. In order to prove congruence using AAS, you must show that all three of the sides in one triangle are congruent to the corresponding sides in another triangle.
This can be difficult if you do not know the lengths of those sides. If you do know the lengths of those sides, then it is usually easier to use ASA because it does not require any angles.
ASA Vs. AAS:
Now you know that both ASA and AAS are used in geometry and trigonometry. Now let’s move on to the differences between the two terms.
ASA and AAS are essentially similar in terms of triangle congruence, but there are also a few differences between ASA and AAS.
Some of the differences are:
- The meaning
When comparing the difference between ASA and AAS, the first difference is that ASA stands for Angle Side Angle. On the other hand, AAS stands for Angle Angle Side. It is as mentioned in the definitions above.
- The purpose
The second difference between ASA and AAS is that ASA is a method of proving congruence whereas AAS is a method of proving similarity.
- Geometry and trigonometry
The third difference between ASA and AAS is that ASA usually uses only geometry whereas AAS uses both geometry and trigonometry.
- Definitions
The fourth difference between ASA and AAS is that ASA is defined as the angles formed by two lines with the same transversal and AAS is defined as the angles formed by two lines with the same transversal and an included angle.
- Visualizing
The fifth difference between ASA and AAS is that ASA can be visualized as the angles formed by two lines with the same transversal and AAS cannot be visualized because it involves an included angle.
- Algebraic manipulation
The sixth difference between ASA and AAS is that ASA can be manipulated algebraically whereas AAS cannot be manipulated algebraically. This is because ASA involves two pairs of congruent angles whereas AAS involves two pairs of similar angles.
- The location of the lines
The seventh difference between ASA and AAS is that ASA involves lines that are parallel whereas AAS involves lines that are intersecting.
- The formula
The eighth difference between ASA and AAS is that ASA involves the formula A=B-C whereas AAS involves the formula C=A-B.
- The values of the angles
The ninth difference between ASA and AAS is that ASA involves the values of the angles between 0° and 180° whereas AAS involves the values of the angles between 0° and 360°.
- Geometric figures
The tenth difference between ASA and AAS is that ASA involves only geometric figures whereas AAS involves both geometric figures and algebraic expressions.
- Vertex angles
The eleventh difference between ASA and AAS is that ASA involves vertex angles whereas AAS involves non-vertex angles.
- Degree of similarity
The twelfth difference between ASA and AAS is that ASA can be used to determine the degree of similarity whereas AAS cannot be used to determine the degree of similarity.