The Rhombus and the Parallelogram are two of the most important shapes in geometry. In geometry, both of these shapes are used to represent a rectangle. They are also used to represent a square.
However, aside from these similarities between the two shapes, there are also some differences between the Rhombus and Parallelogram. In this article, we will discuss the differences between the Rhombus and Parallelogram in detail. We will look at the characteristics of the Rhombus and Parallelogram, what the Rhombus and Parallelogram are used for, how they are used in geometry, and how they are related to each other. So let’s begin.
Summary Table:
| Rhombus | Parallelogram |
| Can be described as an oblong, diamond-shaped figure | Can be described as a rectangle or square with opposite sides parallel to each other |
| The interior angles of a rhombus are always equal to 180° | The interior angles in a parallelogram are always equal to 90° |
| Has two top sides that are called the diagonals | Has two bottom sides that are called the opposite side |
Definitions:
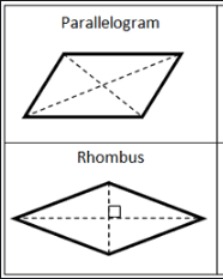
Before we talk about the differences between “rhombus” and “parallelogram”, let’s first define what we mean by “rhombus” and “parallelogram.” To do this, we need to take a look back at the definitions and meanings of these two words, what they are in terms of geometry, and how they are used.
What Is Rhombus?
The Rhombus is a geometric shape that is composed of four right angles. A rhombus has the following characteristics: It is symmetrical, with two pairs of opposite sides being equal in length. The lengths of the opposite sides always add up to the length of one side. A rhombus is a polygon with four sides. It has no interior angles, and it has three sets of opposite angles that are equal in size.
What Is Parallelogram?
The Parallelogram is a shape that consists of two pairs of parallel sides. It is also a symmetrical shape, with two pairs of opposite sides being equal in length. The characteristics are also the same: the lengths of the opposite sides always add up to the length of one side. It also has no interior angles, and it has three sets of opposite angles that are equal in size. In addition, a parallelogram is used to make angles and determine the lengths of certain sides.
How Are Rhombus and Parallelograms Used?
The Rhombus is a shape that is used to make other shapes. For example, it can be used to make a square or rectangle. When this happens, we say that the rhombus is being used as a reference.
When the Rhombus is used to make other shapes, it is said that the rhombus serves as a guide. The shapes that are made by using a rhombus as a guide are called parallelograms.
In addition, the Rhombus is also used to determine angles and lengths. For example, it can be used to make an angle of 45 degrees or an angle that is formed by connecting two points on a line. When this happens, we say that the rhombus is being used as a tool.
Rhombus Vs. Parallelogram:
As you may know, there are several words that have a similar meaning. For example, “rhombus” and “parallelogram” are both used to describe a quadrilateral with four equal sides. These words have a similar meaning, but they are not exactly the same. As mentioned above, the Rhombus and Parallelogram are actually two different shapes that have very different meanings and uses. Let’s take a look at the difference between them now:
The Shape
The Rhombus is a quadrilateral figure that has four equal sides. A rhombus can be described as an oblong, diamond-shaped figure. It is a regular polygon, meaning that it can be constructed by connecting the midpoints of all the sides of a rhombus.
On the other hand, a parallelogram can be described as a rectangle or square with opposite sides parallel to each other. It is also known as a rhombus in some contexts. It is a parallelogram because it is constructed by using a pair of parallel lines.
The Length Of The Sides
The length of the sides of a rhombus is always one half its perimeter, while the length of the sides in a parallelogram is always equal to its perimeter. So if you have a rhombus with sides of length “A”, then the perimeter is “AB”. On the other hand, if you have a parallelogram with sides of length “B”, then its perimeter is “AB + B = AB + B = AB”.
The Shape Of The Top And Bottom Sides
The rhombus has two top sides that are called the diagonals, while the parallelogram has two bottom sides that are called the opposite side. This means that in a rhombus, one diagonal is parallel to one of its sides, while in a parallelogram, one opposite side is parallel to one of its sides.
The Shape Of The Interior Angles
The interior angles of a rhombus are always equal to 180°, while the interior angles in a parallelogram are always equal to 90°. This means that in a rhombus, one interior angle is always opposite to another angle. In a parallelogram, all the interior angles are 90°, as mentioned.
The Uses Of The Rhombus And Parallelogram
Now that you know the difference between a rhombus and parallelogram, let’s look at how they are used in geometry. The rhombus is often used in teaching mathematics because it is one of the simplest shapes to construct with a compass. The rhombus can be constructed by using a compass and a straight edge. You can use the rhombus to demonstrate that all angles are equal to 180°, or you can use it to demonstrate that all sides are equal.
In geometry, the parallelogram is often used in constructing rectangles and squares because they are formed by using two parallel lines. You can use the parallelogram to demonstrate that all angles are equal to 90°, or you can use it to demonstrate that all sides are equal.